3 Comparison sorting algorithms
In the lectures, the concept of Merge Sort, a comparison sorting algorithm, was introduced. The implementation of Merge Sort using arrays as data structures and an out-of-place implementation for the merge part was explained. The pseudocode for the recursive implementation of Merge Sort was analyzed, and the different parts of the algorithm and their tasks were defined. The execution of Merge Sort was simulated with a specific small input, and each step of the algorithm was explained, including the recursive calls and the merge function. The tasks given were to write the pseudocode for the merge function and to calculate the worst and best case time complexity of Merge Sort. The solution document was provided for these tasks, which can be used to check the correctness of the solutions.
3.1 Introduction
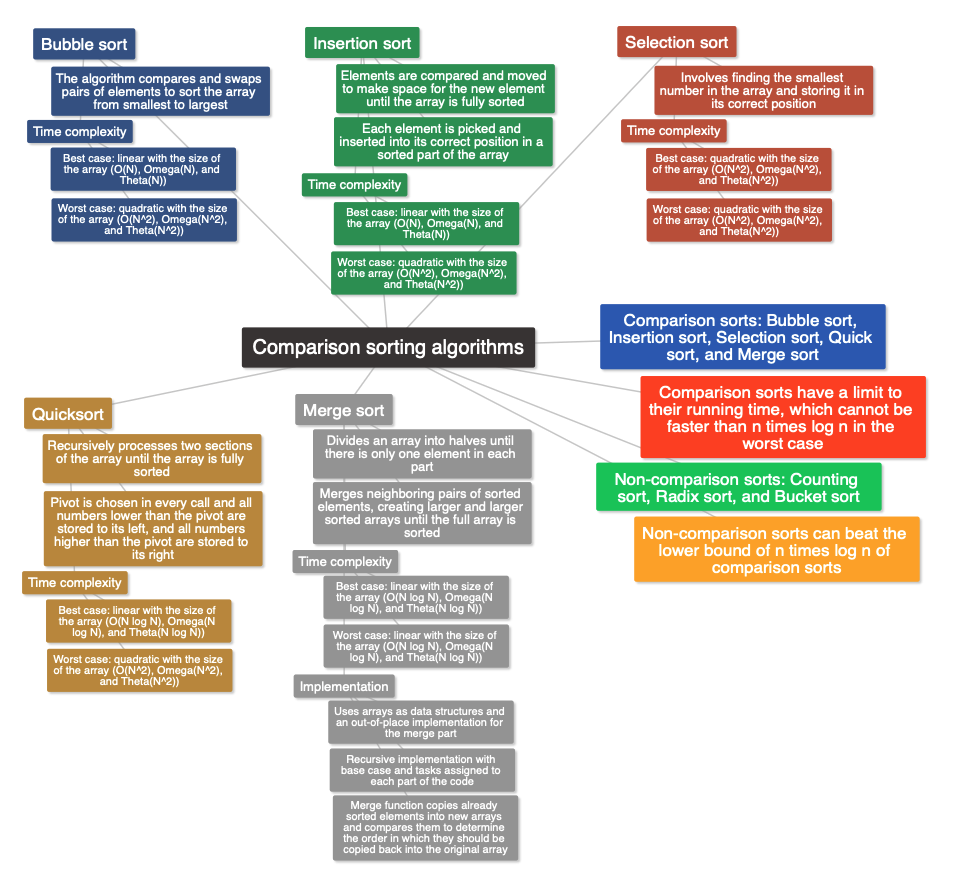
Topic 3 is about sorting in Computer Science, which involves arranging data in ascending or descending order. Sorting algorithms can be classified into two categories, comparison and non-comparison sorts. Comparison sorts, such as Bubble sort, Insertion sort, Selection sort, Quick sort, and Merge sort, compare pairs of elements to determine sorting order. Non-comparison sorts, such as Counting sort, Radix sort, and Bucket sort, do not make comparisons. The main point of learning non-comparison sorts is that comparison sorts have a limit to their running time, which cannot be faster than n times log n in the worst case. The lecture provides a summary of the worst and best case time complexity for the most known comparison sorts and explains that there is no comparison sort that can run faster than n times log n in the worst case. The lecture concludes by saying that non-comparison sorts can beat the lower bound of n times log n of comparison sorts.
3.2 Bubble sort
3.2.1 Bubble sort demonstration
The lecture is about the bubble sort algorithm, which gets its name from how the highest numbers “bubble up” to the highest positions in the array during sorting. The lecture demonstrates the execution of bubble sort on an unsorted array of five numbers, explaining how the algorithm compares and swaps pairs of elements to sort the array from smallest to largest. The lecture goes through each pass of the algorithm until the array is fully sorted, indicating that no more swaps are needed.
3.2.2 Bubble sort pseudo code
The lecture reviews the pseudocode of the bubble sort algorithm, which has a while loop nested in a for loop. The while loop checks if a swap was made during the last pass through the array and if so, continues to execute the for loop. The for loop compares pairs of elements and swaps them if they are in the wrong order. The algorithm sorts the array from smallest to largest. After each pass, the value of n is decreased to avoid comparing already sorted numbers. The lecture includes a step-by-step simulation of the algorithm’s execution on a small input array, demonstrating how the highest numbers bubble up to the highest positions during sorting. Finally, the lecture notes that the time complexity of bubble sort is still theta n to the square in the worst case, despite the fast best-case performance of this implementation.
3.2.3 Bubble sort time complexity
In this lecture, the time complexity of bubble sort is analyzed for both the best and worst cases. In the best case, the array is already sorted, and the time complexity is linear with the size of the array, represented as O(N), Omega(N), and Theta(N). In the worst case, when the array is sorted in reverse order, the time complexity is quadratic with the size of the array, represented as O(N^2), Omega(N^2), and Theta(N^2). The worst-case analysis shows that the algorithm’s running time grows quadratically with the size of the array.
3.3 Insertion sort
3.3.1 Insertion sort demonstration
The lecture explains the concept of insertion sort, where each element in an array is picked and inserted into its correct position in a sorted part of the array. The lecture walks through an example of sorting an array using insertion sort, demonstrating how elements are compared and moved to make space for the new element, until the array is fully sorted.
3.3.2 Insertion sort pseudocode
The lecture reviews the pseudocode for insertion sort and simulates its execution with a small input. The pseudocode involves a for-loop that selects the next element to be inserted in the sorted part of the array and a while loop that determines the correct position to insert the number and moves the numbers to the right to make space. The sorted part of the array is increased in each iteration of the for-loop. The simulation shows how the algorithm sorts an array of five elements. The lecture concludes by inviting the listener to analyze the time complexity of the algorithm for the best and worst cases.
3.4 Selection sort
3.4.1 Selection sort demonstration
In this lecture, the instructor explains the concept of selection sort. Selection sort involves finding the smallest number in the array and storing it in its correct position. The instructor demonstrates the sorting process by visually selecting the smallest number and swapping it with the number in the correct position. The process is repeated until the entire array is sorted. The instructor also notes that the process can be optimized by packing the function that finds the smallest number in one step.
3.4.2 Selection sort pseudo code
The lecture explains the pseudocode of selection sort and simulates its execution using a specific input array. The algorithm works by finding the minimum value in the unsorted portion of the array and placing it in its correct position. This process is repeated until the entire array is sorted. The lecture also answers two questions: 1) Selection sort is a comparison sort, and comparisons are made within the pos_min function. 2) The worst and best case time complexity of selection sort is O(n^2), the same as bubble sort.
3.5 Quicksort
3.5.1 Quicksort demonstration
This lecture covers the idea behind Quicksort, which is one of the two recursive comparison sorting algorithms. In Quicksort, the pivot is chosen in every call and all numbers lower than the pivot are stored to its left, and all numbers higher than the pivot are stored to its right. The execution of Quicksort starts with choosing the pivot, and in this implementation, the highest number is chosen as the pivot. After that, every number lower than the pivot goes to the left part of the array, and every number higher than the pivot goes to the right part of the array. The Quicksort algorithm is then applied recursively on both parts of the array until the array is fully sorted.
3.5.2 Quicksort pseudocode
The lecture discusses quicksort, a comparison sorting algorithm that is easy to code using recursion. Quicksort calls itself twice and recursively processes two sections of the array: the left section from position low to p-1, and the right section from position p+1 to high. The function partition is called for each section and performs three tasks: selecting the pivot, rearranging the array to move all numbers lower than the pivot to its left and all numbers greater than the pivot to its right, and returning the position of the pivot. The execution of quicksort stops when low is no longer lower than high. The lecture provides a simulation of the algorithm execution for a specific input array.
The tasks assigned are to write pseudocode for the function partition, which selects the pivot and rearranges the array, and to calculate the worst and best case time complexity of quicksort using the master theorem.
3.6 Mergesort
The lecture explains the idea behind merge sort, which involves dividing an array into halves until there is only one element in each part. The algorithm then merges neighboring pairs of sorted elements, creating larger and larger sorted arrays until the full array is sorted. The lecture gives an example of a five element array being sorted using merge sort. It is explained how comparisons and merging are done at each step until a sorted array is obtained. The lecture concludes by mentioning that the implementation of merge sort will be covered in the next lecture.
3.6.1 Mergesort demonstration
In this lecture, the execution of Merge sort with a specific small input was simulated, and the step-by-step process was explained in detail. It was emphasized that after executing the first recursive calls, the left half of the array between the positions l and h is already sorted. The execution of the algorithm was completed with the merge function, which copies the left and right halves of the array into two new arrays, sorts them, and merges them back into the original array. The task of writing the pseudocode for the merge function was given, which involves copying already sorted elements into new arrays and comparing them to determine the order in which they should be copied back into the original array. The second task was to calculate the worst and best case time complexity of Merge sort using the master theorem.
3.6.2 Mergesort pseudocode
This lecture is about implementing Merge sort. Merge sort is a comparison sorting algorithm that can be coded easily using recursion. There are different implementations of Merge sort depending on the data structure used to store the numbers and the specific algorithm used for the merge part. This lecture focuses on the implementation that uses arrays as data structures and an out-of-place implementation for the merge part, which uses extra memory space to improve time complexity. The pseudocode for the recursive implementation of Merge sort is analyzed in detail, including the recursive structure, base case, and tasks assigned to each part of the code. The execution of the algorithm is demonstrated step-by-step using a specific example array. The merge function is also briefly introduced.
3.7 Flash cards
Flashcard for “Merge Sort”
Front: What is Merge Sort?
Back: Merge Sort is a comparison sorting algorithm that involves dividing an array into halves until there is only one element in each part. The algorithm then merges neighboring pairs of sorted elements, creating larger and larger sorted arrays until the full array is sorted.
Front: What is the time complexity of Merge Sort?
Back: The worst and best case time complexity of Merge Sort is O(n*log(n)), which is faster than bubble sort, insertion sort, and selection sort in the worst case.
Flashcard for “Comparison and non-comparison sorting algorithms”
Front: What is a comparison sorting algorithm?
Back: A comparison sorting algorithm compares pairs of elements to determine sorting order, such as Bubble sort, Insertion sort, Selection sort, Quick sort, and Merge sort.
Front: What is a non-comparison sorting algorithm?
Back: A non-comparison sorting algorithm does not make comparisons, such as Counting sort, Radix sort, and Bucket sort.
Flashcard for “Bubble sort demonstration”
Front: What is Bubble sort?
Back: Bubble sort is a comparison sorting algorithm that gets its name from how the highest numbers “bubble up” to the highest positions in the array during sorting.
Front: How does Bubble sort work?
Back: Bubble sort works by comparing pairs of elements and swapping them if they are in the wrong order, sorting the array from smallest to largest.
Flashcard for “Insertion sort demonstration”
Front: What is Insertion sort?
Back: Insertion sort is a comparison sorting algorithm that involves selecting each element in an array and inserting it into its correct position in a sorted part of the array.
Front: How does Insertion sort work?
Back: Insertion sort works by comparing elements and moving them to make space for the new element, until the array is fully sorted.
Flashcard for “Selection sort demonstration”
Front: What is Selection sort?
Back: Selection sort is a comparison sorting algorithm that involves finding the smallest number in the array and storing it in its correct position.
Front: How does Selection sort work? Back: Selection sort works by visually selecting the smallest number and swapping it with the number in the correct position, repeating the process until the entire array is sorted.
Flashcard for “Quicksort demonstration”
Front: What is Quicksort?
Back: Quicksort is a comparison sorting algorithm that involves choosing a pivot and storing all numbers lower than the pivot to its left and all numbers higher than the pivot to its right.
Front: How does Quicksort work?
Back: Quicksort works by recursively processing two sections of the array, the left section from position low to p-1, and the right section from position p+1 to high, until the array is fully sorted.
Flashcard for “Mergesort demonstration”
Front: What is the Merge sort algorithm?
Back: Merge sort is a comparison sorting algorithm that involves dividing an array into halves until there is only one element in each part. The algorithm then merges neighboring pairs of sorted elements, creating larger and larger sorted arrays until the full array is sorted.
Front: How does Merge sort work?
Back: Merge sort works by recursively dividing the array into halves, sorting each half, and merging the sorted halves back into the original array until the full array is sorted.