7 Trees
The lecture series covers the concept of trees and hierarchical data structures, binary trees and their implementation, tree traversal techniques like breadth-first and depth-first traversal, binary search trees and their operations, including insert, search, and delete. The lectures also explain the time complexity of each operation and provide pseudocode and examples for implementation. The audience is challenged to think about modifying the algorithms for non-binary trees, maintaining the BST conditions, and balancing binary search trees.
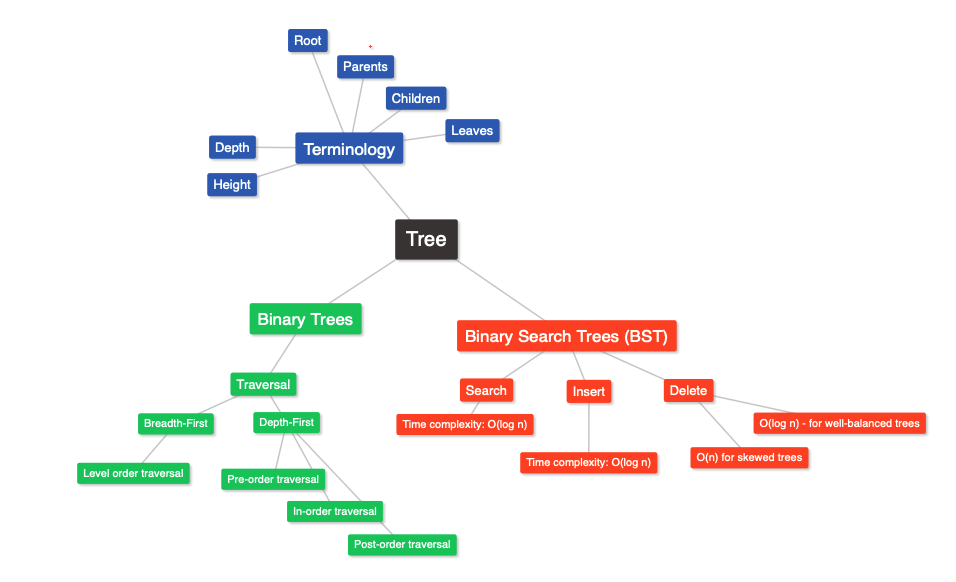
7.1 Introduction
The lecture introduces the concept of hierarchical data structures known as trees, with the root at the top and leaves at the bottom. The nodes in the tree have parents, children, ancestors, and descendants, and each node has a depth and level. The height of the tree is the number of branches from the root to the deepest leaf. Binary trees are a type of tree where each node has at most two children, and they are drawn with the left child to the left of the parent and the right child to the right of the parent. Binary trees are useful for recursive algorithms, and the lecture introduces the topic of binary tree traversal and implementing binary search using binary trees.
7.2 Binary trees implementation
The lecture covers two ways of implementing a binary tree: using memory pointers or using arrays. Memory pointers involve defining a node with three memory spaces to store data and the memory addresses of the left and right children. Array implementation involves storing the root node at position 0 of the array and the elements at Level k using 2_k positions, starting at position 2_k minus 1. Memory pointers use more memory but allow for dynamic growth, while arrays use less memory but have a fixed size. The lecture provides examples of adding nodes to a binary tree using memory pointers and introduces the topic of tree traversal in the next lecture.
7.3 Binary tree traversal introduction
The lecture explains that traversing a binary tree involves visiting all nodes of the tree and is important for operations like insertion, deletion, and search. There are two main approaches to traversing a tree: breadth-first and depth-first. Breadth-first traversal involves visiting nodes from top to bottom and left to right, while depth-first traversal involves visiting nodes vertically, diving into the tree. Depth-first traversal has three types: pre-order, in-order, and post-order, which determine the order of visiting nodes relative to the root node. Pre-order visits the root node first, in-order visits the root node in the middle, and post-order visits the root node last. The lecture provides an overview of the traversal approaches and introduces the topic of implementing breadth-first and depth-first traversal in the next lectures.
7.4 Depth first traversal
In this lecture, the focus was on the implementation of depth-first traversal for binary trees, which includes pre-order, in-order, and post-order traversal. The lecture went through the pseudocode of the pre-order traversal and simulated its execution. It was noted that all three types of traversal are recursive functions and the prefix of their name indicates the order of visiting the root node. The lecture also highlighted the order in which nodes are visited in each type of traversal. Finally, the lecture pointed out that the same recursive structure applies to the sub-trees. In the next lecture, the implementation of breadth-first traversal will be discussed.
7.5 Breadth first traversal
In this lecture, the implementation of breadth-first traversal of a binary tree is studied. The iterative algorithm uses a queue data structure to store the information about nodes to visit. The pseudocode shows how to enqueue nodes, visit them, and store their children information in the queue. The algorithm is executed step by step on a tree as an example. The lecture emphasizes that breadth-first traversal is a horizontal traversal, and it is more comfortable to follow for Western humans, but depth-first traversal is easier to code because it takes advantage of the vertical recursive structure of the tree. The lecture concludes by challenging the audience to think about how to modify the algorithm to work with non-binary trees.
7.6 Binary search trees
In this lecture, the use of binary trees for binary searches was discussed. It was explained that binary search is not efficient in a linked list, and that a binary tree is better suited for binary search. A binary search tree (BST) must meet two conditions: all nodes in the left subtree must store numbers that are lesser than the root, and all nodes in the right subtree must store numbers that are greater than the root. The lecture then ended with a discussion of the operations of a binary search tree, including insert, search, and delete, and the challenges of maintaining the BST conditions during these operations.
7.7 BST insert
In this lecture, the implementation of the insert operation in a binary search tree was discussed. The pseudocode for the insert function was provided, and the process of inserting nodes was demonstrated step by step. The time complexity of the insert operation was analyzed, and it was determined that the worst-case time complexity is theta(n) when the tree is not balanced. The importance of maintaining the rules of a binary search tree, where all nodes in the left subtree are less than the root and all nodes in the right subtree are greater than the root, was emphasized. Finally, it was mentioned that the other two important operations of a binary search tree, search and delete, will be discussed in future lectures.
7.8 BST search
In this lecture, the implementation of the operation search in a binary search tree was discussed. The key idea is that when searching for a number, you take advantage of the fact that all numbers less than the root are stored in the left subtree and all numbers greater than the root are stored in the right subtree. The search function starts by checking whether the number being searched for is in the root. If it is, the function returns true. If it is not, the function recursively searches on either the left or right subtree depending on whether the number being searched for is less than or greater than the root. The time complexity of the search operation is Theta log n, assuming a balanced binary search tree. However, for an unbalanced binary search tree, the worst-case time complexity can be Theta n if all nodes are on one side of the tree. Therefore, for the search operation to have a time complexity of Theta log n, the binary search tree must be balanced.
7.9 BST delete
In this lecture, the operation delete in a binary search tree is discussed. The three cases to consider when deleting a node from a binary search tree are explained. Case 1 is when the node to be deleted is a leaf node with no children. Case 2 is when the node to be deleted has only one child. Case 3 is when the node to be deleted has two children. In Case 3, the minimum value in the right subtree or the maximum value in the left subtree is selected and copied into the node to be deleted, and then the node where the maximum or minimum value was found is deleted. The pseudocode for each case is provided, and the structure of the delete function is discussed in detail. The lecture emphasizes that although deleting a node from a binary search tree is a lengthy function to implement, it becomes easier to understand once the cases are known and the pseudocode is familiar.