5 Hashing
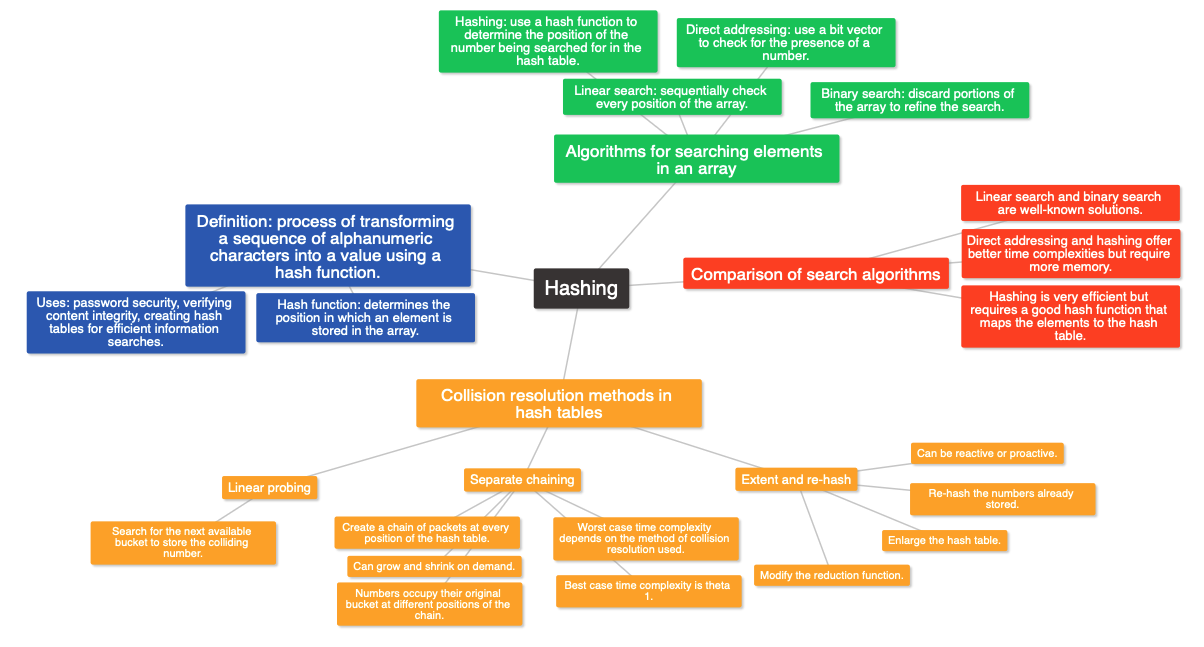
The series lecture introduces hashing, which is the process of transforming alphanumeric characters into a value using a hash function. Hashing is used to efficiently search for elements in an array, with hash tables being widely used in computer science. The lectures covers four algorithmic solutions to searching for an element in an array, including linear search, binary search, direct addressing, and hashing. The lectures also discusses collision resolution in hash tables and presents three methods for dealing with collisions: extent and re-hash, linear probing, and separate chaining. The best case time complexity for hash table operations is theta 1, while the worst case time complexity depends on the method of collision resolution used.
5.1 What is hashing?
Hashing is the process of transforming a sequence of alphanumeric characters into a value using a hash function. Hash functions are used for password security and verifying content integrity in security applications. Hashing is also used to create hash tables for efficient information searches. A hash function is used to determine the position in which an element is stored in the array, and when searching for an element, the hash function is applied to it to quickly determine its position in the array. Hash tables are widely used in computer science.
5.2 Hash tables
The lecture discusses the problem of searching for an element in an array and presents four algorithmic solutions to it: linear search, binary search, direct addressing, and hashing. Linear search and binary search are well-known solutions, with binary search being faster with a time complexity of theta log n in the worst case. Direct addressing and hashing offer even better time complexities of theta 1, but at the cost of memory usage. Hashing, in particular, is very efficient, but its effectiveness depends on having a good hash function that maps the elements to the hash table. The lecture concludes by acknowledging that the efficiency of hashing depends on knowing the elements that will be stored in the hash table beforehand, and that the next lecture will address the issues that arise when this is not the case.
5.3 Collisions in hash tables
This lecture discusses three methods for collision resolution in hash tables: extent and re-hash, linear probing, and separate chaining. Collision resolution is necessary when two or more numbers are hashed to the same position in the hash table. Extent and re-hash consists of enlarging the hash table, modifying the reduction function, and re-hashing the numbers already stored. Linear probing searches for the next available bucket to store the colliding number. Separate chaining creates a chain of packets at every position of the hash table, where the numbers occupy their original bucket at different positions of the chain. The best case time complexity for hash table operations is theta 1, while the worst case time complexity depends on the method of collision resolution used.
5.4 Flash cards
What is hashing?
Hashing is the process of transforming a sequence of alphanumeric characters into a value using a hash function.
What are hash functions used for in security applications?
Hash functions are used for password security and verifying content integrity in security applications.
What are hash tables used for?
Hashing is used to create hash tables for efficient information searches.
What are the four algorithmic solutions for searching for an element in an array?
Four algorithmic solutions for searching for an element in an array are linear search, binary search, direct addressing, and hashing.
Which search algorithm is faster between binary search and linear search?
Binary search is faster than linear search with a time complexity of theta log n in the worst case.
Which two search algorithms offer the best time complexities, and what is the tradeoff?
Direct addressing and hashing offer time complexities of theta 1, but at the cost of memory usage.
What is necessary for the effectiveness of hashing?
The effectiveness of hashing depends on having a good hash function that maps the elements to the hash table.
What are the three methods for collision resolution in hash tables?
Three methods for collision resolution in hash tables are extent and re-hash, linear probing, and separate chaining.
What is the best and worst case time complexity for hash table operations?
The best-case time complexity for hash table operations is theta 1, while the worst-case time complexity depends on the method of collision resolution used.
5.5 Flashcards
Question: What is recursion in computer science? Answer: Recursion is the use of an algorithm that calls itself.
Question: What are the three parts of recursion covered in this topic? Answer: The three parts of recursion covered in this topic are understanding recursion, creating recursive algorithms, and analyzing recursive algorithms.
Question: What is the structure of a well-built recursive algorithm that executes a finite number of recursive calls? Answer: A well-built recursive algorithm that executes a finite number of recursive calls includes a base case to stop the recursion and an input argument that gets closer to the base case with every recursive call.
Question: What is the key takeaway from tracing a recursive algorithm? Answer: Tracing a recursive algorithm can help you understand what task it is performing, even if it is not immediately obvious.
Question: How do recursive algorithms differ from iterative algorithms? Answer: Recursive algorithms call themselves, while iterative algorithms use loops to repeat a set of instructions.
Question: What is the technique used to write recursive algorithms? Answer: The technique used to write recursive algorithms is doing a small part of the job and delegating the rest without caring about the details of how the delegated task is going to be executed.
Question: How is the time complexity of recursive algorithms analyzed? Answer: The time complexity of recursive algorithms is analyzed using recurrence equations.
Question: What is the master theorem? Answer: The master theorem is a method used to analyze the time complexity of recursive algorithms with a specific structure.