8 Heaps
In this series of lectures on heaps, we have learned about various operations related to heaps and how they can be used to implement efficient algorithms.
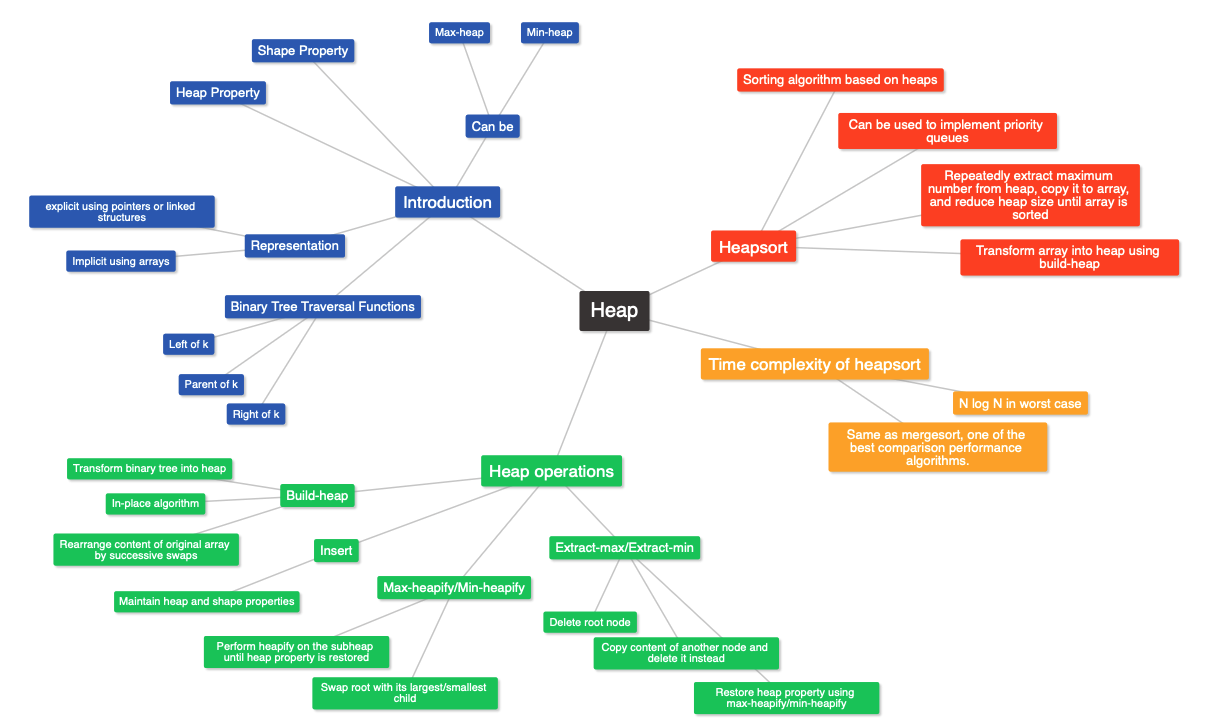
We started by understanding what heaps are and their properties, including the shape property and the heap property. Then, we learned about the various operations on heaps, including insert, extract-max, max-heapify, and build-max-heap. We learned how to implement these operations in pseudocode and understand their time complexities. We also learned about the in-place technique for building a max-heap from an existing binary tree.
Next, we learned about the heapsort algorithm, which is a sorting algorithm built on the principles of heaps. We learned how to implement heapsort in pseudocode, and how to calculate its time complexity. We saw that the worst-case time complexity of heapsort is N log N, which is the same as mergesort and makes it one of the best comparison performance algorithms.
Finally, we learned about the use of heaps in implementing priority queues, where the items are served based on their allocated priority, and how extracting the maximum value from a heap can make this process efficient.
Overall, these lectures have provided a comprehensive understanding of heaps, their properties, and their various applications in computer science.
8.1 Introduction
In this lecture, the speaker explains the concept of a heap, which is a hierarchical data structure that satisfies two properties: the Heap Property and the Shape Property. The Heap Property refers to the relationship between the values of parent and child nodes, which can be either greater or less than, depending on whether the heap is a max-heap or a min-heap. The Shape Property refers to the shape of the tree, which must be a perfect triangle or a triangle with a left-aligned rectangle in the base. The speaker provides examples of both max-heap and min-heap and mentions that heaps can have a maximum of n children. The speaker emphasizes the importance of these properties in implementing heap operations, such as inserting a new number into the heap. The speaker concludes by stating that the next lecture will cover how to implement heaps.
8.2 Implementation
In this lecture, the speaker discusses the implementation of heaps and how they can be represented using arrays, which is an implicit representation. The speaker demonstrates how to move through the heap when implemented using an array and provides algebraic expressions to find the position of a parent and children node in the array. The speaker also introduces three functions - parent of k, left of k, and right of k - that help to move through the implicit heap. The speaker concludes by stating that this knowledge will be useful in the next lecture when discussing the most common operations used to manipulate the data stored in a heap.
8.3 Insert, element by element
The lecture covers the implementation of heaps using arrays, particularly the implicit representation, and the movement through the heap by calculating the positions of the parent and children of a node using algebraic expressions. The lecture then focuses on the insertion operation in a max-heap, demonstrating how to maintain the heap and shape properties while inserting numbers. The lecture also provides pseudocode and step-by-step execution of the insertion operation. Lastly, the lecture tasks the listener with identifying the necessary modifications to transform the function insert for a max-heap to a min-heap and hints about studying the function delete in the next lecture.
8.4 Deletion, extract maximum
The lecture discusses the heap operation that deletes the root node, called extract-max for a max heap or extract-min for a min heap. Deleting another node from the heap is not efficient due to the partially sorted nature of the heap. To delete the root node, we copy the content of another node and delete that node instead. After deleting the root node, we need to recover the heap property using the heapify process. The lecture provides pseudocode for the extract-max and max-heapify functions, which use recursion to swap the root with its largest child and perform heapify on the subheap until the heap property is restored. The lecture also mentions a task to write pseudocode for the index largest node function and the extract-mean and mean-heapify functions for a min heap.
8.5 Build in place
The lecture explains two ways to transform an existing binary tree into a max-heap, namely using either an out-of-place or an in-place algorithm. The focus is on the latter, which involves rearranging the content of the original array by doing successive swaps. The process starts from the bottom up and involves heapifying subtrees at each level, with the leaves being already heaps. The pseudocode for the in-place algorithm is presented, and a step-by-step simulation of it is demonstrated using an input array to show how it transforms the binary tree into a max-heap.
8.6 Heapsort
In this lecture, the HEAPSORT algorithm was introduced as a sorting algorithm built on heaps. The first step is to transform the array into a heap using the build-heap operation in place. Then, the algorithm repeatedly extracts the maximum number from the heap, copies it to the empty position in the array, and reduces the size of the heap until it disappears and the array is sorted. The lecture also mentioned that heaps can be used to implement priority queues, where the next person or process to serve is determined by extracting the maximum number from the heap. Finally, the lecture ended with a note on the time complexity of heapsort, which will be discussed in the next lecture.
8.7 Heapsort’s complexity
In this lecture, the speaker reviews what has been covered so far in the topic of heaps, including the four heap operations (insert, extract-max, max-heapify, and build-heap) and the heapsort algorithm. The speaker then examines the time complexity of heapsort and walks through the pseudocode to calculate the time complexity of build-max-heap and extract-max. The worst-case time complexity of heapsort is N log N, which is the same as that of mergesort, making it one of the best comparison performance algorithms.